Complex Numbers Cubed
The complex number z can be cubed creating the complex number z^3 . We hypothesize that the geometric figure being transformed to z^3 will be rotated another π/2 radians because we are multiplying by another factor of i. We also expect the figure to dilate more since there is another factor of real numbers.
Line Segments
|
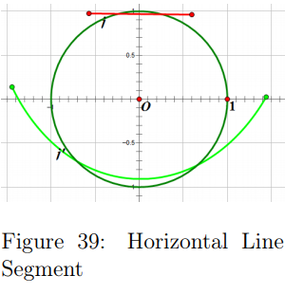
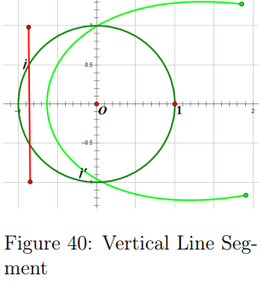
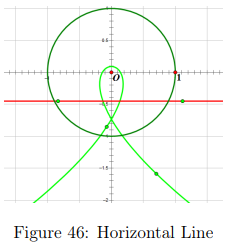
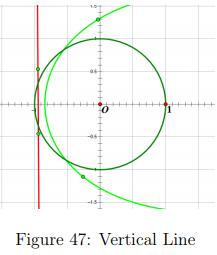
Here we can see that our predictions are true and that the parabolic shape on a closed interval becomes more dilated is rotated to π radians [2]. Seen in Figures 39 and 40. A horizontal pre-image creates a parabolic shape that is vertical and is opened upward and the opposite follows when that line passes the real number axis. A vertical line segment creates a parabola on a closed interval that is horizontal and is opened towards the right and the opposite is created when it crosses the imaginary number axis.
|
|
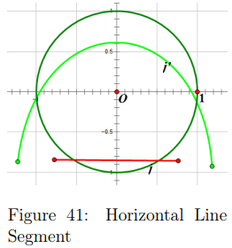
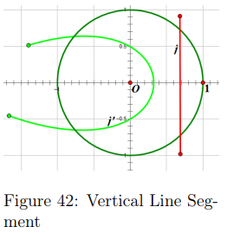
Compared to the transformations of the line segments of z^2 the parabolas are rotated π/2 radians and it creates a more dilated curve. Mathematically this is logical because a function cubed will create a reflection across the line y = x and so that is why after crossing a certain axis the image flips. See Figures 41 and 42.
|
|
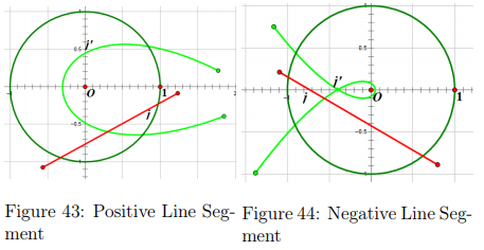
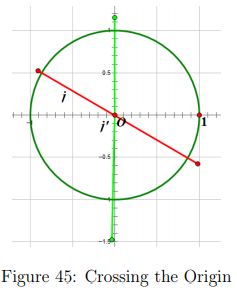
The same principles of rotating and dilating because of the multiplication of a complex number are applied to when the line segment is a positive slope and a negative slope. The image will be like the images of z^2 but it will be rotated another π/2 radians and the line segment will be more dilated. See Figures 43 and 44.
|